Subdivision Surfaces
はじめに
滑らかなサーフェスをモデリングするもっとも一般的な方法は、BスプラインやNURBSなどの 双3次曲面をつなぎ合わせることです。
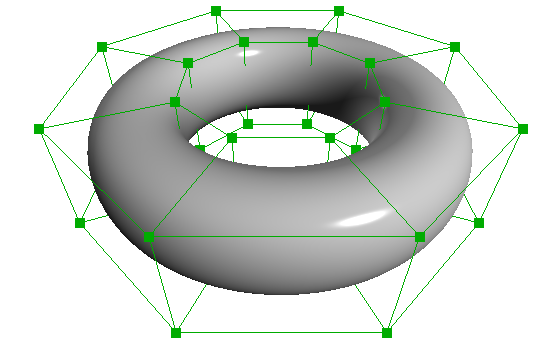
これらはしっかりした滑らかな極限サーフェスを得られますが、双3次サーフェスは トポロジが2次元に限定されるため現実世界のシェイプのごく一部しか記述することができません。 この根本的なパラメータ制約により、オーサリングツールは少なくとも次の機能を持つ必要があります。
ただしトリミングもスティッチングもモデルの滑らかさを保つ必要があり、またそれがアニメーションする 際にも滑らかであり続けなければなりません。これには複雑で負荷の高い計算が必要になってしまいます。
一方サブディビジョンサーフェスはあらゆるトポロジを表現することが出来るため、上記のような 難しさにとらわれることがありません。
任意のトポロジ
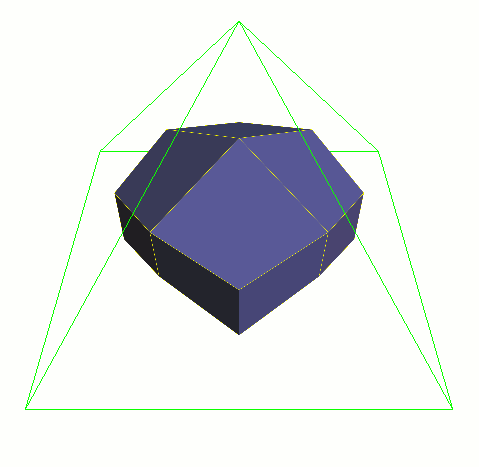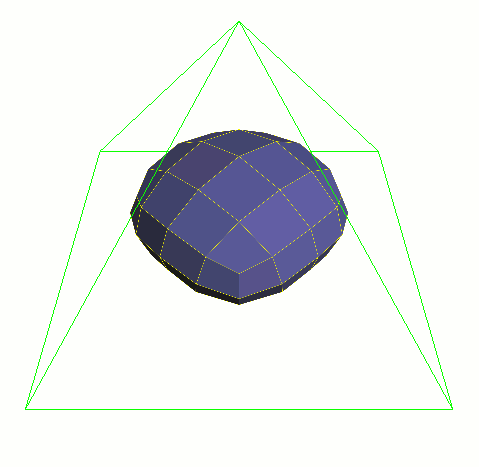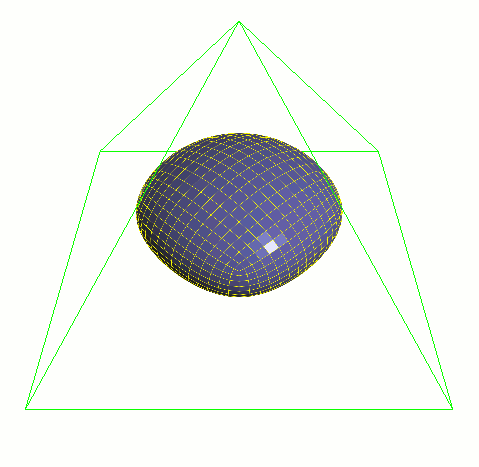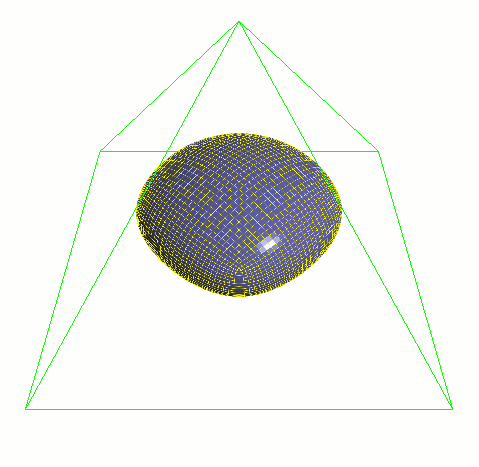
サブディビジョンサーフェスはその他のパラメトリックサーフェスと同様に、コントロール メッシュのポイントで記述されます。サーフェスそれ自体は部分的にスムーズになるように 近似したり補間したりできるのですが、ポリゴンサーフェスを滑らかにするには膨大な量の 頂点が必要になるのに対し、サブディビジョンサーフェスは常に滑らか、つまりどのように 動いてもどれだけ近づいてもポリゴンのアーティファクトは発生しません。
通常の3次Bスプラインサーフェスは格子状のテンソル積パッチです。サブディビジョンサーフェスは これを任意の接続形状のコントロールグリッドに一般化したものになります。



均一分割か、適応型分割か
特徴適応型分割は速度面でもメモリ消費面でも有利ですが、アプリケーションの用途によって選んでください。
以下の表に検討すべき要素を列挙しています。
| Uniform | Feature Adaptive |
|---|---|
|
|
|
|
|
|
Release Notes (3.0.0)
- Full support for bi-cubic face-varying interpolation is a significant feature which will be supported in future releases.
- Feature adaptive refinement for the Loop subdivision scheme is expected to be supported in future releases.
境界補間ルール
境界補間ルールとは、境界エッジと頂点をどのように補間するか制御する方法です。
以下のルールが頂点の補間に適用可能です:
| モード | 挙動 |
|---|---|
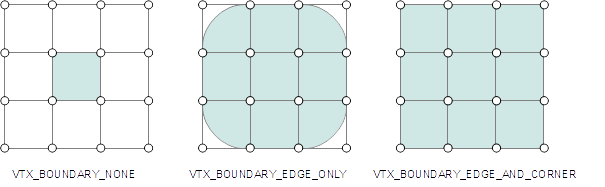
| VTX_BOUNDARY_NONE | 何もしない;境界になる面はホールとして扱われます。 内側の面の連続性のために使われますが、それ自体は極限 サーフェスに含まれません。 |
| VTX_BOUNDARY_EDGE_ONLY | すべてのバウンダリエッジをシャープクリースとする |
| VTX_BOUNDARY_EDGE_AND_CORNER | すべてのバウンダリエッジをシャープクリースとし、面を一つ だけもつバウンダリ頂点をシャープコーナーとする |
グリッドの例:
面変化(Face Varying) 補間ルール
面変化(Face-varying)データはサーフェス上で切れ目があるデータ、主に切れ目のあるUV などに使われます。面変化データは頂点データの補間と同じ規則に従うか、あるいはコーナー、 境界、内部をそれぞれ直線的に補間するか選ぶ事ができます。
面変化データの補間には以下の規則が適用可能です。下の表は直線的な補間になる順にならんでいます。
| Mode | Behavior |
|---|---|
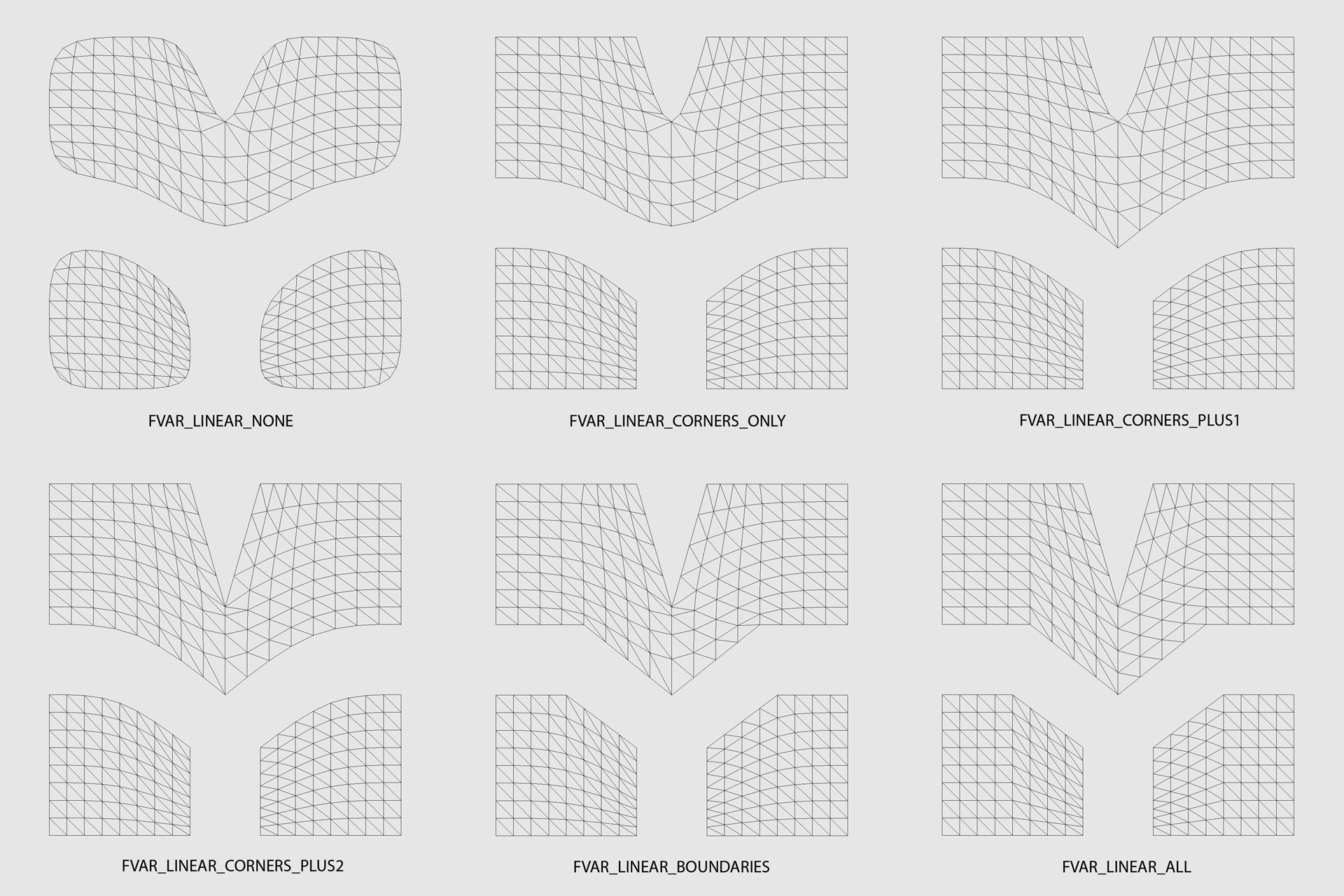
| FVAR_LINEAR_NONE | smooth everywhere the mesh is smooth |
| FVAR_LINEAR_CORNERS_ONLY | sharpen (linearly interpolate) corners only |
| FVAR_LINEAR_CORNERS_PLUS1 | CORNERS_ONLY + sharpening of junctions of 3 or more regions |
| FVAR_LINEAR_CORNERS_PLUS2 | CORNERS_PLUS1 + sharpening of darts and concave corners |
| FVAR_LINEAR_BOUNDARIES | linear interpolation along all boundary edges and corners |
| FVAR_LINEAR_ALL | linear interpolation everywhere (boundaries and interior) |
どの面変化補間ルールを使っても、ベースになる頂点より面変化データを滑らかに補間することはできません。 メッシュのシャープな特徴はシャープネス値、境界補間ルール、スキーム自体が優先します。
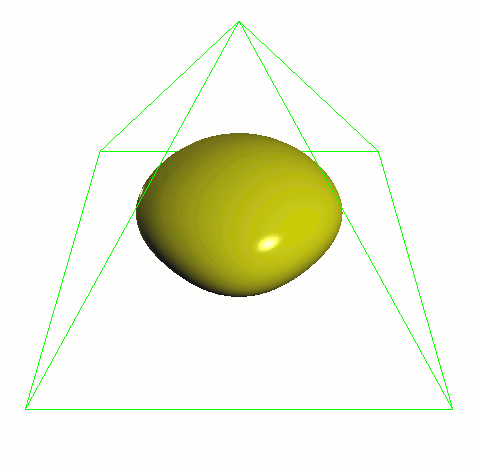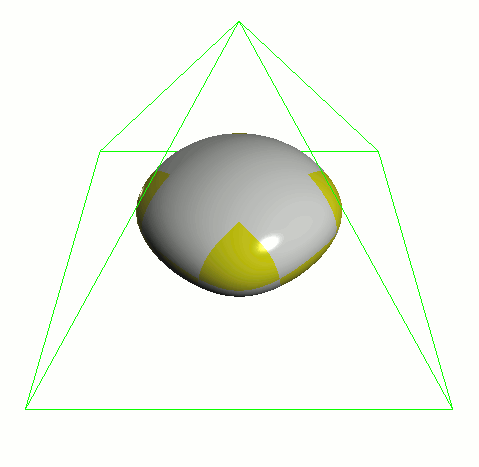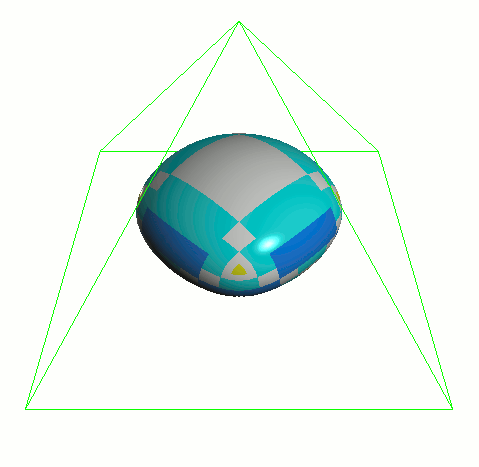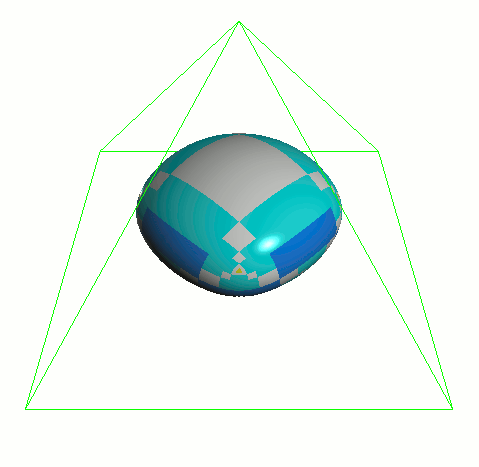
catmark_fvar_bound1 テストシェイプをすべての規則で分割した UV 値の例。このシェイプは 単純な 4x4 グリッドの四角形ですが、3つの UV 領域に分かれています(コントロールポイント の場所は FVAR_LINEAR_ALL の様子でわかります):
セミシャープクリース
サブディビジョン規則を一部変更して部分的に滑らかなサーフェスにクリースやコーナー などの完全にシャープな特徴を作ることができます。特別なケースとしては境界エッジを シャープとタグ付けし、境界を補間することができます。
しかし、現実世界のサーフェスは完全にシャープなエッジというのはありません。このため セミシャープクリースという表現を導入しました。つまり、丸みを帯びた制御可能な シャープネスをもつクリースです。これによりフィレットやブレンドのような特徴を 作ることができます。エッジや連結エッジをクリースでタグ付ける際に、シャープネスの値を 0〜10の範囲で与える事ができます。10 以上のシャープネスは完全シャープとして扱います。
完全シャープクリースでは接線が不連続になり、法線ベクトルも不連続になることに 注意してください。このため法線方向へのディスプレイスメントはクリースにそって 分離してしまいます。クリース部分でディスプレイスメントが必要な場合はセミシャープ クリースをつけるようにしてください。

チャイキン則
チャイキンのカーブ分割アルゴリズムを使って複数エッジに渡るセミシャープ クリースの見た目を改善することができます。チャイキン則はシャープネスを 隣接エッジで補間します。
| モード | 挙動 |
|---|---|
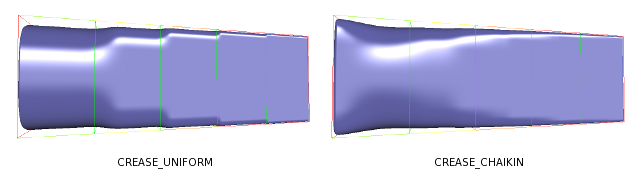
| CREASE_UNIFORM | 通常のセミシャープクリース則を適用 |
| CREASE_CHAIKIN | セミシャープクリース則にチャイキンアルゴリズムを適用 |
連続するセミシャープクリースの補間例:
"三角形サブディビジョン"規則
三角形サブディビジョン規則は Catmull-Clark 分割のオプションで、三角形フェイスの 分割に適用することができます。この規則は経験的に決められたもので、三角形の分割を 滑らかにすることができます。ただし、この規則は2つのメッシュの境界を重ねる ことでシームレスに接続できるという便利な特性をなくしてしまいますので注意してください。
| モード | 挙動 |
|---|---|
| TRI_SUB_CATMARK | 標準の Catmark 重みづけ |
| TRI_SUB_SMOOTH | "スムーズ三角形" 重みを適用 |
シリンダーの例 :

多様体と非多様体ジオメトリ
極限サーフェスを連続に一意に作るためには一般的にはトポロジが二次元多様体で ある必要があります。時として一時的に非多様体ジオメトリをモデリングするのが 便利なこともありますが、その場合には極限サーフェスは定義されません。
以下の例は非多様体ジオメトリを構成する典型的な例です。
非多様体の羽根型形状
次の「羽根型(矢尻型)」のジオメトリは一つのエッジを3つの面で共有しています。
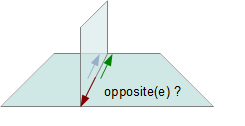
この構造だとどの面が極限サーフェスを構成するのかを決めることができません。 これは3面の場合にかぎらず、3面以上の面がエッジを共有するときには同じ 問題が発生します。
非多様体エッジは、「部分的に多様体」な領域を考慮して取り扱われます。複数の面を 含む問題があるエッジを補間して通過する極限サーフェスのかわりに、そのエッジで複数の極限 サーフェスを幾つかに分割します。こうして面がそれぞれ極限サーフェスを持ち (部分的に多様体)、エッジでつながる、というような処理になります。